[TOC]

杂题选刷

记录一下自己最近做的题吧

P6619 冰火战士

树状数组+二分/线段树

P6619 [省选联考 2020 A/B 卷] 冰火战士

• $10pts$

不离散化，直接暴力

• $20pts$

最优解一定在某个战士的温度值取到。

这就是考场上导致我没有想出$60pts$的原因（第二个就是没注意到2操作也要输出答案，浪费$1$个小时$debug$）

暴力枚举温度，暴力更新即可

复杂度:$O(Q^2)$，期望得分：$20pts$

• $60pts$

树状数组+二分

还是先可以离散化一下温度，设$I[t]$为在$t$温度下冰战士的能量和，$F[t]$是火战士的能量和，答案就是$2\cdot\min(I(t),F(t))$

则显然有$I(t)$单调不降$F(t)$单调不增

我们可以二分一个$I(t)$和$F(t)$最接近的合适的温度，分别用两个树状数组维护冰和火战士（一个前缀和，一个后缀和）

复杂度为$O(Q*log^2Q)$，期望得分：$60pts$

• $100pts$

现在还不会，以后更新

代码见P6619 [省选联考 2020 A/B 卷] 冰火战士

P4062 Yazid 的新生舞会

思路题+线段树/树状数组

淦，我之前写的东西没保存

P4062 Yazid 的新生舞会

给定一长度为$n$的序列，求有多少子序列$[l,r]$的众数出现$\frac{r-l+1}{2}$次

• 算法一（针对$n\leq 300$）

考虑枚举所有区间，然后求其众数及出现次数，并判断是否超过区间总长的一半，统计答案即可。时间复杂度$O\left( n^3\right)$

• 算法二（$n\leq 2,000$）

考虑先枚举区间的左端点$l$，再从左到右枚举右端点$r$并用数组维护每个数的出现次数，同时使用变量维护当前众数、众数的出现次数。不难发现，当右端点向右移动时，这些信息都是非常方便维护的。于是我们便可以在$O\left( n^2\right)$的时间复杂度内统计所有答案。

• 算法三（$type=1$）

对于$01$序列，我们不难发现，众数出现次数严格大于子区间长度当且仅当子区间内$0,1$出现次数不同（那么那个出现次数较多的就是众数）。于是我们将原序列中的$0$视作$-1$，并对该序列求前缀和$S$，则子区间$[l,r]$为“新生舞会的”，当且仅当$S_r-S_{l-1}\not= 0$

有了这个性质我们就可以$O(1)$来求解子区间$[l,r]$是不是符合要求了，但是不幸的是这样仍需要枚举$l,r$，复杂度仍是$O(n^2)$。

我们不妨反着来想，子区间$[l,r]$不是“新生舞会的”，当且仅当$S_r-S_{l-1}=0$即$S_r=S_{l-1}$因此对$S$进行排序并从小到大统计相等的个数然后用总的子区间数量$\frac{n\cdot(n+1)}{2}$减去相等的个数即为答案

• 算法四（$type=2$）

对于所有数的出现次数都较小（不超过$15$）的情况，不难发现所有“新生舞会的区间”的长度也会较小（不超过$2\times 15-1=29$）。于是使用算法二，枚举所有长度少于$30$的区间并统计答案即可。

• 算法五（$type=3$）

对于$A_i\leq 7$的测试点，我们不妨枚举所有值作为众数的情况。考虑统计所有众数为$k$的“新生舞会的”区间，将所有等于$k$的位置取为$1$，不等于$k$的位置取为$-1$，得到新序列$B$并求前缀和得到序列$S$，则区间$[l,r]$需要被统计，当且仅当$S_r-S_{l-1}\geq 1$。从左到右枚举右端点，并用线段树维护当前右端点左边每种前缀和出现的次数即可。时间复杂度$O\left( 8nlogn\right)$

• 算法六（$100pts$）

考虑改进算法五。我们考虑取出所有$B$中的极长$-1$子区间，观察这些区间中的所有点作为右端点对答案的贡献。不难发现极长$-1$子区间$[l,r]$中的所有点作为右端点对答案的贡献为$\sum_{i=1}^{r-l+1}\sum_{j=-\infty}^{S_{l-1}-i-1}cnt[j]$，其中$cnt[j]$表示在区间$[0,l-1]$之间前缀和为$j$的端点数目；在统计这段区间的答案后，我们还需要对区间$[S_{i-1}-(r-l+1),S_{i-1}-1]$中的所有$cnt$均进行$+1$操作。显然地，我们使用一个维护$B_i$和$C_i=i\times B_i$的线段树就可以支持这些查询、修改操作。于是我们使用这棵线段树维护相关信息，并从左到右枚举右端点，统计答案即可。

不难发现，极长$-1$子区间的数目与序列中$k$的数目同阶，因此，对于统计众数为$k$的“新生舞会的”区间的时间开销，不难发现我们通过上述优化将时间开销缩短到了$O\left( 序列A中k的数目\log{n}\right)$

于是，总时间复杂度即为$O\left(\sum_{k} 序列A中k的数目\log{n}\right)$，即$O\left(n\log{n}\right)$。

51Nod 1327 棋盘游戏

区间dp

1327 棋盘游戏

给定$n\cdot m$的方阵，每个格子可以填$1$或者$0$，求每一列最多只有$1$个$1$，第$i$行从左开始向右连续$left[i]$个格子只有$1$个$1$，从右边开始向左连续$right[i]$个格子只有$1$个$1$的方案数

读完题感觉有点像$CSPday2$的题，怪

有一种浓浓的区间$dp$的味道，这道题的显然不能按照行来做（行的限制比较多，很难搞），所以我们应该按照列来定义状态$f[i][j][k][0/1]$为到第$i$列，左边的列填了$i$个$1$，右边的列填了$j$个$1$，当前列有没有$1$，这样转移不了啊

我们可以思考每一列可以放的情况：如果一些行的左区间的终点在该列，那么这些行是必然要被放的（不然就不符合要求了），如果一些行的右区间从这一列开始，那么没有处理完的行就会多出几个，放到后面的状态处理即可，还有一种情况就是选择$left$和$right$之间的部分放一个$1$

如下图（ps:图画的不太对，蓝线应该在格子里，自己$YY$吧，我懒得改了）所示，在蓝色线那一列，第$1$,$2$,$4$,$6$的红色必定已经填过了，而且黄色的第$1,2$行可以填了，第$4,6$行就是可以选择$left$和$right$之间的部分放一个$1$的情况

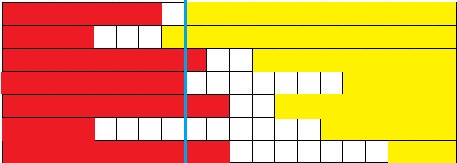
那么状态就可以定义了$f[i][j][k]$表示到了第$i$列，在这之前有$j$列没有放过妻子，且已经有$k$行到了有区间(黄色部分)

记$l_i,r_i,mid_i$分别表示第$i$行左区间右端点为$i$，右区间左端点为$r_i$，第$i$列没有覆盖住的行数

根据上面的分析：每一列的转移要添加$r_{i+1}$的右区间放置机会，要将$l[i+1]$全部搞定。
则转移为：

• 放在红色格子

$f[i+1]\left[j+1-l_{i+1}\right]\left[k+r_{i+1}\right]+=f[i][j][k] * A_{j+1}^{l_{i}+1}$

• 放在黄色格子

$f[i+1]\left[j-l_{i+1}\right]\left[k+r_{i+1}-1\right]+=f[i][j][k] * A_{j}^{l_{j+1}} *\left(k+r_{i+1}\right)$

• 放在白格子

$f[i+1]\left[j-l_{i+1}\right]\left[k+r_{i+1}\right]+=f[i][j][k] * A_{j}^{l_{i+1}} * m i d_{i+1}$

51Nod 1683 最短路

1683 最短路

随机$01$矩阵，对每个$k$求$(1,1)\sim(n,m)$最短路为$k$的概率，路径长度指的是不能向左走前提下路径上权值为$1$的格子个数。$n\leq6,m\leq100$

一个显然的性质：相邻两格子最短路值相差不超过$1$

剩下的我不会了......以后再做吧

51Nod 1843 排列合并机

1843 排列合并机

看不懂题，弄不懂样例，告辞

老师给安排的题目也太难了吧，我都不会（自闭ing

P5970 Nim z utrudnieniem

博弈论+dp

Nim z utrudnieniem

$A$和$B$在进行$Nim$博弈，$A$是先手，但是$B$在开始之前可以扔掉$d$的倍数堆的石子（不能扔掉全部的），问$B$有多少种扔的办法使$B$必胜。

显然$B$必胜的条件为$a_1 \oplus a_2 \oplus \cdots a_n = 0$($NIM$博弈的结论)

显然可以这么来定义状态$f[i][j][k]$表示前$i$堆石子，扔掉了$j$堆(在$mod\ d$下),异或和是$k$的方案数

$f[i][j][k]=f[i-1][j][k]+f[i-1][j-1][k\oplus a_i]$

复杂度为$O(n\cdot d\cdot maxa_i)$

现在的问题在于怎么把$maxa_i$这一项变小？

有一个神奇的结论

因为对于任意一个正整数$N$，它和比它自己小的数字异或起来的结果不会超过$N \times 2$

所以只需要把$a_i$从小到大排序，这样复杂度就变成$O(m\cdot d)$

现在问题在于空间开销太大了。

显然可以用滚动数组，但是仍然太大，因为我们必须要把$i$这一维给省掉。

只需要在每一层$i$时，按照$k$从大到小的顺序进行转移即可。

还要注意$n$是$d$的倍数时，会算上全选的情况，答案需要减去$1$

代码见P5970 Nim z utrudnieniem 题解

P4042 [AHOI2014/JSOI2014]骑士游戏

有后效性的dp

$$\large\text{要用魔法打败魔法}$$

P4042

一共有$n$种不同的怪物，每种怪物都可以用两种方式杀死，第一种消耗$s_i$体力将怪物变成另外一种或多种怪物，第二种消耗$k_i$体力，可以直接杀死，问最少消耗体力杀死$1$号怪物

读完题之后感觉是个图的模型，但是建了一下图发现不太好建边，更不太好跑最短路。（淦

那就从$dp$角度来思考一下。

设$f[i]$杀死第$i$号怪需要的最小体力，显然有$f[i]=\min(k_i,s_i+\sum\limits_{j=1}^{R_i}f[r_{i,j}])$，$r_{i,j}$表示用蛮力杀死$i$后分裂的第$j$个。

经过了上面的建图过程就会发现，可能会存在环(也就是有后效性)，到时候就死了。(淦$\times2$

现在大概只能在$dp$的式子上下手了，显然后效性在$dp$式子后面的一项上。

当且仅当$\forall f[r_{i,j}]<f[i]$，$f[i]$才能被后面一项更新，我们不妨换一个角度来进行转移，用某一个$f$值去更新其他的$f$。

一个更显然的性质，对于$k_i$最小的怪物，$f[i]=k_i$，所以我们对$f$建立一个堆，然后每次弹出一个点$i$来更新其他的$f_{r_{i,j}}$，如果更新完了，则就把$f_{r_{i,j}}$放到堆里（这样就确保了不会有后效性）

代码见骑士游戏

P3592 [POI2015]MYJ

区间dp

P3592

有$n$家洗车店从左往右排成一排，每家店都有一个正整数价格$p[i]$。有$m$个人要来消费，第$i$个人会驶过第$a[i]$个开始一直到第$b[i]$个洗车店，且会选择这些店中最便宜的一个进行一次消费。但是如果这个最便宜的价格大于$c[i]$，那么这个人就不洗车了。请给每家店指定一个价格，使得所有人花的钱的总和最大。

因为每个人不洗车的当且仅当$[l_i,r_i]$中最小的$p[i]>c[i]$，所以有个显然的性质：每个商家价格是$c[i]$一定是最优解之一。因此我们可以将$c[i]$离散化。

用$f[l][r][i]$表示区间$[l,r]$内最小值是$i$，从满足$l\le a \le b\le r$的人中获得的最大收益

枚举区间最小值所在的点$k$，则满足$l\le a\le k$且$k \le b\le r$的点最小位置就是$k$，统计出$c\ge i$的人有几个

$f[l][r][i]=\max\limits_{l\le k\le r}\{realc_i\times cnt+\max\limits_{h\ge i}f[l][k-1][h]+\max\limits_{h\ge i}f[k+1][r][h]\}$

代码见P3592 [POI2015]MYJ

CF319E Ping-Pong

并查集+线段树

CF319E Ping-Pong

规定区间$(a,b)$到区间$(c,d)$有边当且仅当$c<a<d$或$c<b<d$。

起初区间集合为空。有$n$（$n\leq 10^5$）次操作，每次操作形如：

• 1 x y（$|x|,|y|\leq10^9$）：加入一个新区间$(x,y)$，保证新区间长度最长
• 2 x y：询问第$i$个加入第区间能否到达第$j$个加入第区间，保证询问合法

连边的两种情况：第一种是包含，小的向大的连边；第二种是相交不包含，连双向边。

注意到答案最后不会走超过$1$条单向边

所以可以用并查集维护，用线段树拆分区间，然后连边

P4132 [BJOI2012]算不出的等式

思路题

P4132 [BJOI2012]算不出的等式

给定奇质数$p,q$，求$\sum\limits_{k=1}^{\frac{p-1}{2}}\left\lfloor\frac{k q}{p}\right\rfloor+\sum\limits_{k=1}^{\frac{q-1}{2}}\left[\frac{k p}{q}\right]$

读完题之后，看不懂这个式子是求了个什么东西，算了，还是打表看题解吧

这么恶心人的式子竟然就是求直线下方点的个数，我佛了

该式两部分分别是一个$(\frac{p-1}{2},\frac{q-1}{2})$方格图主对角线分成的两部分的整点